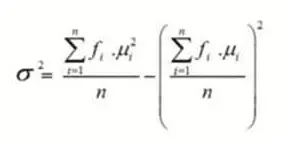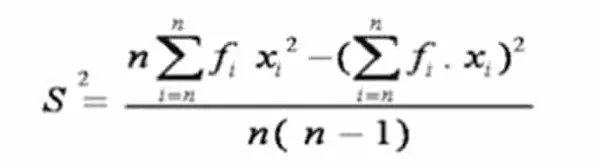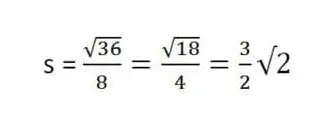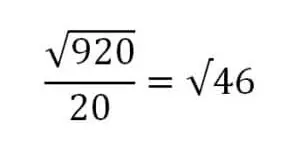RUMUS STANDAR DEVIASI – Standar deviasi kerap disebut dengan istilah simpangan baku. Hampir serupa dengan varian, standar deviasi juga menjadi ukuran variasi atau dispersi.
Pun, standar deviasi menjadi ukuran dispersi yang paling sering digunakan. Penyebabnya adalah standar deviasi memiliki satuan ukuran yang tidak berbeda dengan satuan ukuran data asal.
Semisal, jika terdapat satuan data asal berupa cm, maka satuan dalam standar deviasi adalah cm. Berlaku juga untuk jenis satuan yang lainnya.
Standar deviasi yang diperuntukkan bagi populasi adalah σ, sedangkan bagi sampel, simbolnya adalah s.
Untuk mengetahui tentang rumus standar deviasi, sila simak pengertian, dan hal-hal penting terkait dengannya terlebih dahulu!
Definisi
Pengertian dari standar deviasi yakni ukuran penyebaran yang paling banyak dipakai. Segala gugus data pun dipertimbangkan supaya lebih stabil.
Standar deviasi merupakan ukuran yang paling stabil ketimbang ukuran yang lainnya. Akan tetapi, jika dalam gugus data ada nilai ekstrem, maka standar deviasi tidak lagi sensitif seperti yang terjadi pada mean.
Standar deviasi juga dapat diartikan sebagai ukuran-ukuran keragaman atau variasi dari data statistik yang kerap digunakan.
Yang mana rumus standar deviasi diambil dari akan kuadrat varian. Maka dari itu, apabila salah satu nilai dua ukuran itu diketahui, maka nilai ukuran yang lainnya pun dapat diketahui.
Dari rumus standar deviasi tersebut, dapat disimpulkan bahwa semakin rendah nilainya, maka semakin data mendekati rata-rata.
Sedangkan apabila nilai standar deviasinya tinggi, maka semakin lebar juga rentang dari variasi data.
Untuk itu, standar deviasi adalah besarnya perbedaan nilai sampel pada rata-rata.
Standar deviasi disimbolkan dengan sigma σ yang diambil dari alfabet Yunani. Bisa juga dengan huruf latin s.
Standar deviasi dalam Bahasa Inggris disebut dengan standard deviation.
Contoh kasus penghitungan rumus standar deviasi adalah semisal saat Anda akan mengetahui nilai yang diperoleh siswa pada suatu kabupaten berpopulasi 50.000 orang siswa, lalu diambil sampel sebanyak 5.000 siswa.
Maka, dengan riset sampel, akan diperoleh data dengan standar deviasi tersendiri.
Apabila standar deviasi semakin besar, maka keragaman sampelnya juga semakin banyak.
Fungsi
Biasanya, standar deviasi digunakan oleh ahli statistik supaya dapat mengetahui apakah sampel data sudah mewakili semua populasi.
Selain itu, fungsinya adalah sebagai berikut:
- Memberi gambaran mengenai persebaran data pada data rata-rata.
- Memberi gambaran tentang kualitas data sampel yang didapatkan sehingga diperoleh kesimpulan apakah dapat mewakili data populasi ataupun tidak.
- Bisa memberi gambaran mengenai rentang nilai minimal serta maksimal pada data yang didapatkan.
- Di perhitungan fisika, bisa memberi gambaran nilai ketidakpastian ketika melakukan pengukuran yang berulang.
Mencari data secara tepat bagi populasi cukup sulit dilakukan.
Untuk itu, gunakan sampel data yang dapat mewakili semua populasi, sehingga, penelitian atau tugas bisa dilakukan secara mudah.
Rumus Standar Deviasi
Masuk ke rumus standar deviasi, setidaknya, ada empat rumus yang terdapat pada ukuran ini. Mari mengeceknya satu per satu:
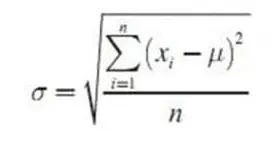
- Rumus Standar Deviasi Data Tunggal
- Rumus Standar Deviasi Data Populasi
- Rumus Standar Deviasi Data Kelompok Sampel
- Rumus Standar Deviasi Data Kelompok Populasi
Keterangan terkait rumus standar deviasi di atas meliputi:
σ2 : varian satu ragam bagi populasi
fi : frekuensi
xi : titik tengah
s2 : varian satu ragam bagi sampel
x– : Rata-rata sampel
n : jumlah data
μ : rata-rata populasi
Cara Penghitungan Standar Deviasi
Terdapat setidaknya 3 metode penghitungan standar deviasi. Mulai dari secara manual, menggunakan Excel, dan juga kalkulator.
Untuk menghitung rumus standar deviasi secara manual, ada dua langkah yang harus dilakukan.
Untuk data tunggal, maka harus mencari nilai rata-ratanya terlebih dahulu. Selanjutnya, cari lah standar deviasi tunggal menggunakan rumus yang telah diterakan di poin sebelumnya.
Selain itu, untuk menghitung standar deviasi, juga terdapat dua rumus yang mesti diketahui yaitu rumus dari varian dan juga standar deviasi.
Nah, yang membutuhkan cara khusus untuk menghitungnya adalah dengan Excel.
Untuk itu, yang akan dibahas secara lebih rinci adalah penghitungan menggunakan Excel.
Menghitung Rumus Standar Deviasi di Excel
Untuk menghitung standar deviasi pada Excel, maka dibutuhkan STDEV. Semisal, terdapat contoh kasus yakni:
Berdasar pada sampel nilai ujian di SMP Bahagia, data yang diketahui adalah: 80, 60, 80, 90, 70, 80, 95. Maka, untuk menghitung standar deviasi pada data menggunakan Excel, caranya adalah:
Buka aplikasi Excel, lalu masukkan data pada tabel.
| DATA | |
| A | 80 |
| B | 60 |
| C | 80 |
| D | 90 |
| E | 70 |
| F | 80 |
| G | 95 |
| STDEV | 11,70 |
Pada baris bagian bawah adalah nilai standar deviasi.
Anda hanya perlu menekan tombol +STDEV(number1 ; number 2; number 3; dan seterusnya).
Jadi, Excel akan menghitung standar deviasi secara otomatis.
Keterangan:
- STDEV mengasumsikan jika argumen merupakan contoh populasi. Apabila data mewakili semua populasi, maka penghitungan standar deviasi memakai STDEVP.
- Standar deviasi dihitung dengan metode “n-1”.
- Nilai logis serta representasi teks dari nomor yang diketik secara langsung pada daftar argumen akan dihitung.
- Apabila argumen merupakan referensi atau array, maka hanya angka pada referensi atau array yang dihitung. Sel kosong, teks, nilai logis, maupun nilai kesalahan pada array akan diabaikan.
- Argumen bisa berupa nama, nomor, referensi, serta array yang mengandung angka.
- Argumen dengan kesalahan teks maupun nilai tidak dapat diterjemahkan dalam angka sehingga bisa menyebabkan suatu kesalahan.
- Apabila akan dimasukkan nilai logis maupun representasi teks angka pada referensi untuk bagian perhitungan, pakai fungsi STDEVA.
BACA JUGA : 6 Poin Penting ROE Sekaligus Rumus ROE
Contoh Aplikasi Rumus Standar Deviasi
Berikut adalah contoh penghitungannya agar Anda bisa lebih memahami cara penghitungannya:
1. Tentukan simpangan baku dari data tunggal berikut! 5, 9, 7, 6, 7, 8, 12, 10.
Pertama, Anda tentukan terlebih dahulu rumus yang akan digunakan. Nah, untuk mencari simpangan baku, maka rumusnya adalah:
Jika sudah, maka cari hasil dari mean atau rata-ratanya terlebih dahulu.
Mean = 5 + 9 +7 + 6 + 7 +8 + 12 + 10 / 8
Maka hasilnya menjadi 64/8 = 8
Kemudian, terapkan rumusnya, terlebih dahulu cari bagian pembilangnya :
(5 – 8)2 + (9 – 8)2 + (7 – 8)2 + (6 – 8)2 + (7 – 8)2 + (8 – 8)2 + (12 – 8)2 + (10 – 8)2 = 9 + 1 + 1 + 4 + 1 + 1 + 4 + 1 + 0 + 16 + 4 = 36
Langsung diterapkan pada rumus di atas :
2. Tentukan simpangan baku dari data kelompok berikut ini!
| Nilai | f |
| 63 – 67 | 2 |
| 68 – 72 | 3 |
| 73 – 77 | 6 |
| 78 – 82 | 4 |
| 83 – 87 | 4 |
| 88 – 92 | 1 |
Gunakan rumus berikut ini untuk menghitung standar deviasi dari populasi:
Selanjutnya, cari nilai dari n dengan menjumlahkan semua nilai dari f, sehingga n hasilnya adalah 20.
Setelah itu, cari nilai tengah(xi), sehingga hasilnya:
| Nilai | f | xi | fixi |
| 63 – 67 | 2 | 65 | 130 |
| 68 – 72 | 3 | 70 | 210 |
| 73 – 77 | 6 | 75 | 450 |
| 78 – 82 | 4 | 80 | 320 |
| 83 – 87 | 4 | 85 | 340 |
| 88 – 92 | 1 | 90 | 90 |
Kemudian, jumlahkan nilai dari fixi sehingga nilainya menjadi 1.540
Masukkan rumus standar deviasi rata-rata berikut ini :
Sehingga hasilnya adalah = 1540/20 = 77
Selanjutnya, carilah nilai dari xi – 77, cari juga nilai dari fi (fi (xi – x)2 hasilnya adalah:
| Nilai | f | xi | fixi | xi – x | Fi (xi – x)2 |
| 63 – 67 | 2 | 65 | 130 | -12 | 288 |
| 68 – 72 | 3 | 70 | 210 | -7 | 147 |
| 73 – 77 | 6 | 75 | 450 | -2 | 24 |
| 78 – 82 | 4 | 80 | 320 | 3 | 36 |
| 83 – 87 | 4 | 85 | 340 | 8 | 256 |
| 88 – 92 | 1 | 90 | 90 | 13 | 169 |
Sigma Fi (xi – x)2 nilainya adalah 920.
Kemudian masukkan rumus yang telah disebutkan di awal, maka hasilnya adalah:
Demikian pembahasan mengenai rumus standar deviasi dan cara menghitungnya. Semoga mudah dipahami dan bermanfaat!